Дядя Богдан и Проекции
Возвращаясь на берег, дядя Богдан зачастую посещает компьютерный клуб «Скала», чтобы порешать там задачи в приятной компании. Однажды, Дядя Богдан встретился там с одним старым знакомым. Этот знакомый задал ему необычную задачу...
На плоскости с декартовой системой координат даны $n$ непересекающихся горизонтальных отрезков с концами в целых точках. Все отрезки находятся строго над осью $OX$. Вы можете выбрать произвольный вектор с координатами ($a$, $b$), где $b < 0$ и координаты — вещественные числа, и спроектировать все отрезки на ось $OX$ вдоль этого вектора. При этом полученные проекции должны не пересекаться, но, возможно, могут касаться.
Вам нужно найти минимально возможную разницу между координатой $x$ правого конца самой правой проекции и координатой $x$ левого конца самой левой проекции.
В первой строке задано одно целое число $n$ ($1 \le n \le 2000$) — количество отрезков.
В $i$-й из следующих $n$ строк заданы три целых числа $xl_i$, $xr_i$ и $y_i$ ($-10^6 \le xl_i < xr_i \le 10^6$; $1 \le y_i \le 10^6$) — абсциссы концов отрезка и их ордината.
Гарантируется, что отрезки не пересекаются и не касаются.
Выведите минимальную разницу, которую можно получить.
Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность не превосходит $10^{-6}$.
Формально, пусть ваш ответ равен $a$, а ответ жюри равен $b$. Ваш ответ будет зачтен, если и только если $\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}$.
3 1 6 2 4 6 4 4 6 6
9.000000000
3 2 5 1 4 6 4 7 8 2
6.333333333
2 1 3 1 4 7 1
6.000000000
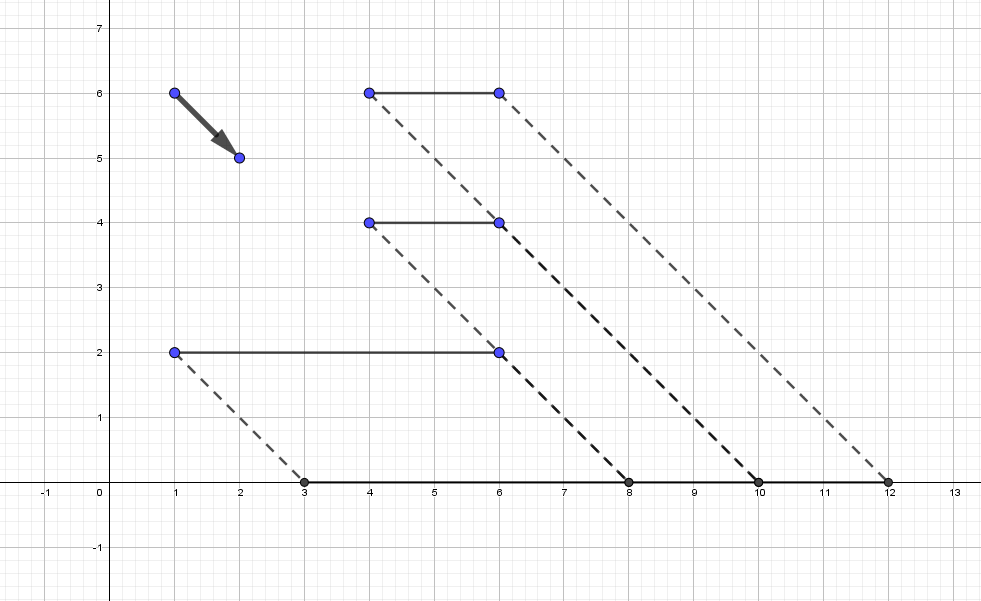
Если в первом примере спроектировать отрезки вдоль вектора $(1, -1)$, который изображен на рисунке, то мы получим ответ $12-3=9$, и можно доказать, что меньше получить нельзя.
Во втором примере оптимально проектировать вдоль вектора $(1, -3)$. Ответ: $8\frac{2}{3}-2\frac{1}{3}=6\frac{1}{3}$

Задача на Codeforces (контест 1388, задача E, © Codeforces.com)